Found this tutorial video for easy multiplication.
Wednesday, September 17, 2014
Tuesday, June 24, 2014
Method to calculate the Square of the numbers with the unit digit 1
Inorder to calculate the square of the numbers with their unit digit " 1", just add the square of the previous number, the previous number and the number given.
For example,
11 ^ 2 = 10 ^ 2 + 10 + 11 = 100 + 10 + 11 = 121
91 ^ 2 = 90 ^ 2 + 90 + 91 = 8100 + 90 + 91 = 8281
Thanks, Numbersmania -Where MATHS is Life Facebook Page.
For example,
11 ^ 2 = 10 ^ 2 + 10 + 11 = 100 + 10 + 11 = 121
91 ^ 2 = 90 ^ 2 + 90 + 91 = 8100 + 90 + 91 = 8281
Thanks, Numbersmania -Where MATHS is Life Facebook Page.
Wednesday, April 2, 2014
Mystery Number
 that satisfies these two properties:
that satisfies these two properties:- The digits of
 add up to a number
add up to a number 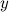 where
where  equals
equals 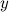 times the number you get when you reverse the digits of
times the number you get when you reverse the digits of 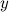 .
. - Reverse the digits of
 and
find the prime factors of the number you get. Then take the sum of the
squares of these prime factors and halve it. Removing the digit 0 from
the new number yields back
and
find the prime factors of the number you get. Then take the sum of the
squares of these prime factors and halve it. Removing the digit 0 from
the new number yields back  .
.
 is a four digit number.
is a four digit number.http://plus.maths.org/content/mystery-number
Solution
The answer is 1729. The number is known as the Hardy-Ramanujan number after Ramanujan and the mathematician and Godfrey Hardy. It has another interesting property: you can write it as a sum of cubes in two different ways:![\[ 1729 = 1^3+12^3=9^3+10^3. \]](http://plus.maths.org/MI/156ac033b85eac55f3b1a25a755a78ad/images/img-0001.png) |
 Srinivasa Ramanujan, 1887-1920.
Srinivasa Ramanujan, 1887-1920.http://plus.maths.org/content/mystery-number
Tuesday, March 4, 2014
Mathematical Anagrams
An anagram is a word or phrase made up of the letters of another word.
These are all made up from maths words.
Friends, Kindly post the answers in the comment.
Source: Mathsphere math puzzles
These are all made up from maths words.
Friends, Kindly post the answers in the comment.
Source: Mathsphere math puzzles
Thursday, February 20, 2014
An Intelligence test

How is this possible ?
The sum of the numbers form the last two digits and the difference between the numbers form the first digit.
Saturday, January 11, 2014
Peculiar Numbers
| The 3 digit numbers 407 and 370 have this peculiarity, that they exactly equal the sum of the cubes of their digits. Thus the cube of 4 is 64, the cube of 0 is 0, and the cube of7 is 343. Add together 64, 0, and 343, and you get 407. Again, the cube of 3 (27), added to the cube of 7 (343), is 370. Can you find a number not containing a zero that will work in the same way? |
Solution:
The other Numbers are 153 , 371.
153 = 1 ^ 3 + 5 ^ 3 + 3 ^ 3 = 1 + 125 + 27 = 153
371 = 3 ^ 3 + 7 ^ 3 + 1 ^ 3 = 27 + 343 + 1 = 371
Other numbers whose cube value are also same as the original number are 0 and 1.
0 = 0 ^ 3 = 0
1 = 1 ^ 3 = 1
Friends, If you could find any other such numbers...kindly let me know.
Thanks,
Multiplication Puzzle
Here
is a simple multiplication puzzle. It is not
difficult, if properly attacked:
A x B = B, B x C = AC, C x D = BC, D x E = CH, E x F = DK, F x H = CJ, H x J = KJ, J x K = E, K x L = L,
A x L = L.
Every letter represents a different digit form 0 to 9, and, of course, AC, BC, etc., are two-figure numbers. Can you find the values in figures of all the letters?
Friends, I have tried a solution for this puzzle. Don't have any idea if it's the correct solution. If you could find any other solutions, kindly let me know.
Thank you,
A x B = B 1 x 3 = 3
B x C = AC 3 x 5 = 15
C x D = BC 5 x 7 = 35
D x E = CH 7 x 8 = 56
E x F = DK 8 x 9 = 72
F x H = CJ 9 x 6 = 54
H x J = KJ 6 x 4 = 24
J x K = E 4 x 2 = 8
K x L = L 2 x 0 = 0
A x L = L 1 x 0 = 0
So, the value of each letter is,
A = 1
B = 3
C = 5
D = 7
E = 8
F = 9
H = 6
J = 4
K = 2
L = 0
A x B = B, B x C = AC, C x D = BC, D x E = CH, E x F = DK, F x H = CJ, H x J = KJ, J x K = E, K x L = L,
A x L = L.
Every letter represents a different digit form 0 to 9, and, of course, AC, BC, etc., are two-figure numbers. Can you find the values in figures of all the letters?
Friends, I have tried a solution for this puzzle. Don't have any idea if it's the correct solution. If you could find any other solutions, kindly let me know.
Thank you,
A x B = B 1 x 3 = 3
B x C = AC 3 x 5 = 15
C x D = BC 5 x 7 = 35
D x E = CH 7 x 8 = 56
E x F = DK 8 x 9 = 72
F x H = CJ 9 x 6 = 54
H x J = KJ 6 x 4 = 24
J x K = E 4 x 2 = 8
K x L = L 2 x 0 = 0
A x L = L 1 x 0 = 0
So, the value of each letter is,
A = 1
B = 3
C = 5
D = 7
E = 8
F = 9
H = 6
J = 4
K = 2
L = 0
Subscribe to:
Comments (Atom)
