 that satisfies these two properties:
that satisfies these two properties:- The digits of
 add up to a number
add up to a number 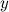 where
where  equals
equals 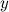 times the number you get when you reverse the digits of
times the number you get when you reverse the digits of 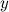 .
. - Reverse the digits of
 and
find the prime factors of the number you get. Then take the sum of the
squares of these prime factors and halve it. Removing the digit 0 from
the new number yields back
and
find the prime factors of the number you get. Then take the sum of the
squares of these prime factors and halve it. Removing the digit 0 from
the new number yields back  .
.
 is a four digit number.
is a four digit number.http://plus.maths.org/content/mystery-number
Solution
The answer is 1729. The number is known as the Hardy-Ramanujan number after Ramanujan and the mathematician and Godfrey Hardy. It has another interesting property: you can write it as a sum of cubes in two different ways:![\[ 1729 = 1^3+12^3=9^3+10^3. \]](http://plus.maths.org/MI/156ac033b85eac55f3b1a25a755a78ad/images/img-0001.png) |
 Srinivasa Ramanujan, 1887-1920.
Srinivasa Ramanujan, 1887-1920.http://plus.maths.org/content/mystery-number